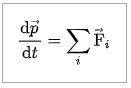Isaac Newton

Accueil du site - Les grands astronomes - Isaac Newton

L'Angleterre n'ayant alors pas encore adopté le calendrier grégorien, la date de naissance d’Isaac Newton est enregistrée en date du 25 décembre 1642 (6 janvier 1643 pour la France avec le calendrier grégorien), au manoir de Woolsthorpe près de Grantham, dans le Lincolnshire en Angleterre, de parents fermiers. Il naît trois mois après la mort de son père.

Figure emblématique des sciences, il est surtout reconnu pour :

• La loi de la gravitation universelle. Il démontre les mouvements des objets sur Terre et des corps célestes sont gouvernés par les mêmes lois naturelles ; en se basant sur les lois de Kepler sur le mouvement des planètes, il développa la loi universelle de la gravitation.


• En mécanique, il a établi les trois lois universelles du mouvement qui constituent en fait des principes à la base de la grande théorie de Newton concernant le mouvement des corps, théorie que l'on nomme aujourd'hui « mécanique newtonienne » ou encore « mécanique classique ».


• En optique, il a développé une théorie de la couleur fondée sur l'observation selon laquelle un prisme décompose la lumière blanche en un spectre visible.


• Il invente télescope à réflexion composé d'un miroir primaire concave appelé télescope de Newton.


• La généralisation du théorème du binôme.


• Il crée en concurrence avec Gottfried Wilhelm Leibniz, le calcul infinitésimal.


• L'invention dite de la "méthode de Newton" permettant de trouver des approximations d'un zéro (ou racine) d'une fonction réelle d'une variable réelle.


• Il a aussi effectué des recherches dans les domaines de la théologie et de l'alchimie.

Son ouvrage "Philosophiae naturalis principia mathematica", publié en 1687, est une œuvre majeure dans l'histoire des sciences. Il y décrit la loi universelle de la gravitation, formule les trois lois universelles du mouvement et jette les bases de la mécanique classique.

En 1704, il publie son ouvrage fondamental d'étude de la lumière, "Optiks", dont il démontre la nature composée. Il y démontre que la lumière blanche est formée de plusieurs couleurs et déclare qu'elle est composée de particules ou de corpuscules. De plus, il ajoute que lorsqu'elle traverse un milieu plus dense, elle est réfractée par son accélération. À un autre endroit de son traité, il explique la diffraction de la lumière en l'associant à une onde.

Dates clé

• 25 décembre 1642 : (julien) - 6 janvier 1643 (grégorien) Naissance.


• 4 juin 1661 : Il entre au Trinity College à Cambridge.


• En 1663 et 1664, Newton découvre les mathématiques dans Miscelanea de Schooten, la Geometria de Descartes, les Clavis mathematica de William Oughtred et les travaux de John Wallis.


• En 1664, il écrit dans Quelques questions philosophiques : « Platon est mon ami, Aristote est mon ami, mais ma meilleure amie est la vérité. »


• En janvier 1665, il obtient un titre de bachelier ès arts et envisage de préparer la maîtrise.


• En 1665, l'Angleterre subit une épidémie de peste noire, si bien que l'université ferme ses portes à l'été 1665 et renvoie les étudiants chez eux. Newton part pour Woolsthorpe, c'est là qu'il progresse fortement en mathématiques, physique et surtout optique.


• En 1666, il entame en 1666 l’étude des fonctions dérivables et de leurs dérivées à partir du tracé des tangentes sur la base des travaux de Fermat. Il classifie les cubiques et en donne des tracés corrects avec asymptotes, inflexions et points de rebroussement.


• En 1668 , il obtient le titre de Master of Arts qui comporte l'obligation de prendre les ordres au sein de l'Église anglicane pour une durée minimale de sept ans.


• En 1669 :
  - Il rédige un compte rendu sur les fondements du calcul infinitésimal qu’il appelle « méthode des fluxions ». Newton a fondé ainsi l’analyse mathématique moderne.
  
  - Il succède à son maître Barrow — qui s'était démis pour se consacrer exclusivement à la théologie — et reprend sa chaire de professeur lucasien de mathématiques.


• En 1671, il améliore un instrument d'optique de son époque, le télescope à réflexion de Gregory. Il invente le télescope à réflexion par miroir concave, naturellement dépourvu d'aberration chromatique, connu sous le nom de télescope de Newton.


• En 1672, à l’âge de 29 ans, sur invitation, Newton présente à la Royal Society son télescope à réflexion qui surpasse tellement tout ce que l'on sait faire à l'époque qu'il entre à la Royal Society de Londres, où il fera la rencontre de Robert Boyle, homme très influent. Il réussit l’exploit de mettre au point un télescope à miroir sphérique dépourvu d’aberration chromatique.


• En 1673, il prend la décision de divulguer grandement ses travaux sur la lumière, ce qui le rend célèbre d’un seul coup. Cette célébrité fait de ses découvertes l’objet de nombreuses controverses et querelles dont il a horreur.


• En 1675, dans son ouvrage Opticks (publié en 1704), il expose ses travaux sur la lumière et prouve qu’elle est constituée d’un spectre de plusieurs couleurs, à l’aide de son prisme. Il complète ses travaux en exposant sa théorie corpusculaire.
• En 1684, par l’astronome britannique Edmond Halley — découvreur de la célèbre comète homonyme — à propos des lois de Kepler sur les orbites elliptiques des planètes. Newton répond de manière convaincante et Halley le pousse à publier ses travaux, en finançant même la publication de son ouvrage.
• En 1687 :
  - Il publie donc son œuvre majeure : Philosophiæ naturalis principia mathematica, (Principes mathématiques de la philosophie naturelle). Cette œuvre marque le début de la mathématisation de la physique. En effet, Newton y expose le principe d’inertie, la proportionnalité des forces et des accélérations, l’égalité de l’action et de la réaction, les lois du choc, il y étudie le mouvement des fluides, les marées, etc. Mais il expose aussi et surtout sa théorie de l’attraction universelle. Les corps s’attirent avec une force proportionnelle au produit de leur masse et inversement proportionnelle au carré de la distance qui les sépare. La simplicité et l'efficacité de cette théorie aura une très forte influence sur les autres sciences au xviiie siècle, particulièrement les sciences sociales comme nous le verrons. Toutefois, sur le moment, si le livre est bien accueilli en Grande-Bretagne, sur le continent la réaction est hostile.
  
  - Il défend les droits de l'université de Cambridge contre le roi Jacques II. Cette action lui vaut d'être élu membre du parlement britannique en 1689 quand le roi, vaincu, doit s'exiler. Durant son mandat, il est très actif dans les débats.
• En avril 1696, il démissionne du Collège de Cambridge pour devenir directeur de la Maison de la Monnaie (Royal Mint), qui lui apporte une amélioration substantielle de son statut économique et social. Au contraire de ses prédécesseurs, il prend son travail très au sérieux et fait notamment emprisonner une centaine de faux-monnayeurs.

• En 1699, il est nommé membre du conseil de la Royal Society puis, après la mort de Robert Hooke, en est élu président — fonction qu'il conservera à vie — en novembre 1703.
• En 1705 :
  
  - Il est anobli par la reine Anne, peut-être moins en raison de ses travaux scientifiques ou de son rôle à la Monnaie que de la proximité d'élections. Il adopte alors un blason inhabituel constitué d'une paire de tibias humains croisés sur un fond noir, à la manière d'un drapeau de pirate sans tête de mort.
  Malgré ses succès dans le domaine du calcul et de la science en général, Newton préfère reprendre, au cours de ses dernières années, ses études de théologie. Il étudie à fond la chronologie des prophéties bibliques et écrit des textes sur les hérésies antiques et les religions païennes.
  
  - Pendant ces années d'études religieuses, sa santé se détériore gravement. À des problèmes mineurs, tels que les calculs rénaux ou la faiblesse des sphincters, viennent s'ajouter une inflammation pulmonaire et une sévère attaque de goutte. Les problèmes respiratoires l'obligent à s'installer à la campagne où son état s'améliore sensiblement.
• En 1727, Newton, à peine remis d’une crise de goutte, se rend à Londres pour présider une réunion de la Royal Society. Ce voyage le fatigue terriblement. De retour dans sa propriété campagnarde de Kensington, il doit rester alité.
• Il meurt le 31 mars 1727, à l'âge de 84 ans. Ses funérailles sont somptueuses. Son cercueil, exposé dans l'abbaye de Westminster, est porté en grande pompe et inhumé dans la nef aux côtés des rois d’Angleterre.

La loi universelle de la gravitation

En janvier 1684, Robert Hooke, Christopher Wren et Edmond Halley débattent sur le mouvement des planètes. Les trois hommes conviennent que le Soleil attire les planètes avec une force inversement proportionnelle au carré de leur distance. La question qu'ils se posent est celle de l'orbite que suivra une planète soumise à l'influence de cette force ; en s'abritant derrière les lois de Kepler, ils imaginent que ce sera une ellipse, mais ils manquent d'outils pour le démontrer.

En novembre, Halley reçoit un bref manuscrit de neuf pages intitulé "De motu corporum in gyrum" (Du mouvement des corps en orbite) où il trouve ce qu'il attendait, et beaucoup plus que cela : une ébauche de la science générale de la dynamique. Halley reçoit l'autorisation de Newton pour commenter à la Royal Society l'œuvre qui, incorporée au tome I des Principia, paraîtra deux ans plus tard.

Newton découvre ainsi la loi universelle de la gravitation ou de l'attraction universelle en tant que cause des mouvements des planètes, unifiant ainsi la mécanique terrestre et la mécanique céleste. Il exprime cette loi de manière simplifiée par l'expression mathématique suivante :

• u→ est le vecteur unitaire indiquant la direction du mouvement,
• F→ est la force de gravitation,
• G est la Constante gravitationnelle,
• Ma et Mb représentent la masse de chacun des corps en présence,
• AB² est le carré de la distance qui sépare ces deux corps.

Newton avait mûri au fil des années cette théorie du mouvement des planètes. Ainsi, dès l'époque de l'épidémie de peste — vers 1665 —, il avait commencé à étudier l'attraction du Soleil sur les planètes. Puis il passa à l'étude de la Lune, mais avec les données sur la Terre dont il disposait à l'époque, les calculs ne tombaient pas juste. Lorsque, en 1675, furent publiés les calculs plus exacts des mesures terrestres réalisés par l'astronome français Jean Picard (1620-1682), il put reprendre ses calculs et vérifier que l'hypothèse était juste. Sa vision du mouvement des corps célestes continua d'évoluer et, au milieu de la décennie 1680, il avait généralisé la théorie de l'action à distance à presque tous les phénomènes de la nature. À cette époque, il vivait complètement immergé dans son œuvre.

Selon la loi de la gravitation de Newton, la gravitation n'est pas seulement une force exercée par le Soleil sur les planètes, mais tous les objets du cosmos s'attirent mutuellement, ajoutant que les planètes ne parcourent pas deux fois la même orbite.

La mécanique céleste, qui repose sur les trois lois de Kepler et la loi universelle de la gravitation de Newton, suffit, encore aujourd'hui, à expliquer par le calcul les mouvements des astres dans un univers local, tel que le système solaire !

La force d'attraction gravitationnelle entre deux masses ponctuelles Ma et Mb est directement proportionnelle au produit des masses et inversement proportionnelle au carré de la distance qui les sépare. C'est ce qu'on appelle une loi en carré inverse.

L'intensité du champ gravitationnel est directement proportionnelle à la masse à l'origine du champ et inversement proportionnelle au carré de la distance.

La force d'attraction gravitationnelle est attractive. Elle dépend uniquement des masses impliquées et de la distance entre elles. Tout corps dans l'univers attire tout autre corps avec une force dirigée suivant la droite passant par les centres de gravité de ces deux corps.

Par exemple, si on multipliait par deux la distance entre la Terre et la Lune, la force d'attraction entre elles diminuerait (à cause de la proportionnalité inverse) d'un facteur 4 au lieu d'un facteur 2à cause du carré. Cette loi décrit autant les objets en chute libre que les corps en orbite circulaire, par exemple un satellite autour de la Terre.

On oublie souvent que la gravitation signifie que tous les objets s'attirent. Il y a une force d'attraction gravitationnelle entre tout couple de masses. Chaque personne est donc attirée par la personne qui se trouve à ses côtés, par son animal de compagnie ou encore par sa pizza, sous l'effet de l'attraction gravitationnelle.

On a tendance à oublier que r est la distance entre les centres de gravité. Il faut mesurer la distance entre les centres de gravité des deux corps considérés, et non entre leurs surfaces.

Les lois du mouvement

La première loi de Newton

« Tout corps persévère dans l'état de repos ou de mouvement uniforme en ligne droite dans lequel il se trouve, à moins que quelque force n'agisse sur lui, et ne le contraigne à changer d'état. »

Autrement dit, s'il n'y a pas de force qui s'exerce sur un corps N 1, ou si la somme des forces s'exerçant sur lui est égale au vecteur nul N 2, sa vitesse est constante (la direction, le sens et la norme sont constants) ou, ce qui revient au même, son accélération est nulle. Cette loi infirme la théorie du mouvement de la physique d'Aristote selon laquelle l'absence de force exercée sur une chose, ou dans les termes d'Aristote l'absence de moteur d'une chose, impliquait l'absence de mouvement de cette chose, son immobilité. En somme sans moteur (ce qui meut) pas de mobile (ce qui est mu).

Le mouvement considéré par Newton a lieu par rapport à un espace mathématique abstrait qu'il suppose absolu. Sa première loi s'applique également dans des référentiels en translation uniforme par rapport à cet espace absolu, appelés référentiels galiléens. Au xixe siècle, la notion d'espace absolu est peu à peu abandonnée au profit des seuls référentiels galiléens. La première loi de Newton se reformule donc aujourd'hui sous la forme :

Dans un référentiel galiléen, le vecteur vitesse du centre d'inertie d'un système est constant si et seulement si la résultante des vecteurs forces qui s'exercent sur le système vaut le vecteur nul.

La deuxième loi de Newton

L'énoncé original de la deuxième loi de Newton est le suivant :

« Les changements qui arrivent dans le mouvement sont proportionnels à la force motrice ; et se font dans la ligne droite dans laquelle cette force a été imprimée. »

Dans sa version moderne, on la nomme principe fondamental de la dynamique (PFD), parfois appelée relation fondamentale de la dynamique (RFD), et s'énonce ainsi :

Dans un référentiel galiléen, la dérivée de la quantité de mouvement p→ d'un solide est égale à la somme des forces extérieures F_i → qui s'exercent sur le solide :

La troisième loi de Newton

L'énoncé original est le suivant :

« L'action est toujours égale et opposée à la réaction ; c'est-à-dire, que les actions de deux corps l'un sur l'autre sont toujours égales, et dans des directions contraires. »

De manière moderne, on exprime que :

Tout corps A exerçant une force sur un corps B subit une force d'intensité égale, de même direction mais de sens opposé, exercée par le corps B. A et B étant deux corps en interaction, la force F_A/B → (exercée par A sur B) et la force F_B/A → (exercée par B sur A) qui décrivent l'interaction sont directement opposées et portées par la droite (AB).

La théorie de la couleur

Newton en 1666 a été le premier à expliquer la décomposition de la lumière par un prisme et sa recomposition avec un second prisme. Il décompose le spectre lumineux, arbitrairement, en sept couleurs. Initialement, il distingue cinq couleurs, et ajoute plus tard, dans son ouvrage majeur sur la lumière (Opticks, 1702) l'orange et l'indigo par analogie avec les sept degrés de la gamme diatonique. Les croyances ésotériques et l'importance symbolique du nombre sept dans la religion et l'histoire ont certainement contribué à ce choix arbitraire.

Voir l'étude détaillée réalisée par Claude Guthmann, professeur émérite de physique à l'Université Paris-Denis Diderot (Paris VII)
Accès au document

Le télescope de Newton

En 1671, il améliore un instrument d'optique de son époque, le télescope à réflexion de Gregory. Conséquence de son étude de la réfraction — la dispersion des couleurs —, il conclut que tout télescope à réfraction ou lunette astronomique présente une dispersion de la lumière ou aberration chromatique, qu'il pense impossible de corriger. Il résout cependant le problème en inventant le télescope à réflexion par miroir concave, naturellement dépourvu d'aberration chromatique, connu sous le nom de télescope de Newton. On sait depuis Chester Moore Hall et surtout John Dollond que l'aberration chromatique peut être compensée en utilisant plusieurs lentilles en verres d'indices de réfraction différents.

En 1671, Isaac Barrow assiste à une réunion de la Royal Society et présente le télescope de Newton, qui plonge l'assistance dans la stupeur. En plus d'éviter l'aberration chromatique, l'appareil inventé par Newton obtient un meilleur agrandissement, bien qu'il soit de petite taille — le premier télescope qu'il a construit mesure environ 15 cm de long et augmente pourtant quarante fois le diamètre de l'image.

En 1672 et sur invitation, Newton présente à la Royal Society son télescope à réflexion qui surpasse tellement tout ce que l'on sait faire à l'époque, qu'il lui permet d'y entrer par la grande porte le 11 janvier 1672. Le plus grand souci de la Royal Society est d'éviter qu'un étranger ne copie le télescope. Un mois après son élection comme membre de la Royal Society, Newton envoie au secrétaire de cette institution un traité sur les couleurs, dans lequel il élabore un schéma de sa théorie en s'appuyant sur trois expériences.

Accueil - Liens utiles - Contact

.