Les lois de Képler

Accueil du site

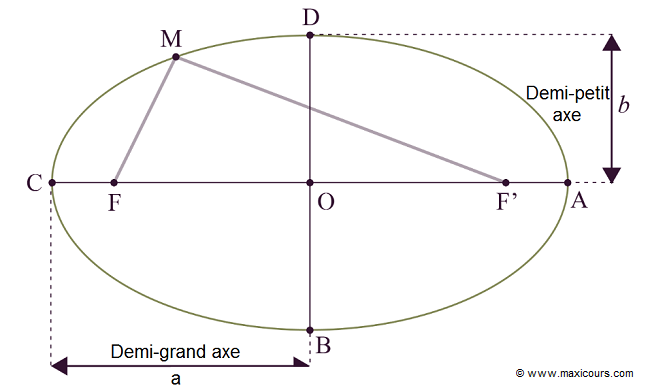
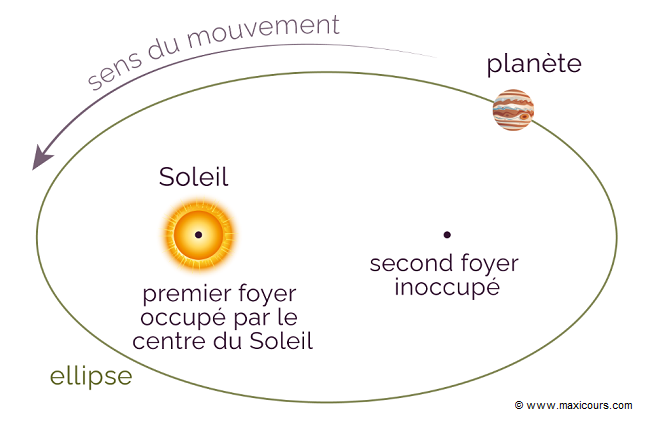
Johannes Kepler (1571-1630), très grand calculateur et mathématicien, eut la chance de prendre la suite de Tycho Brahe dont il analysa les observations. Il découvrit ses lois grâce à un travail d'analyse considérable des tables astronomiques établies par Tycho Brahé. En particulier l'étude de Mars lui permit de montrer que le mouvement n'était pas épicyclique mais elliptique.
Kepler fut donc capable d'en déduire les orbites des planètes et d'énoncer les lois qui portent son nom et qui caractérisent ces orbites. Il introduisit pour la première fois la notion d'orbite elliptique, rompant avec les sacro-saints mouvements circulaires uniformes érigés en dogme par les Grecs. Kepler montra par ailleurs que les plans des orbites planétaires passaient par le Soleil et non par la Terre, ce qui contredisait un des postulats du géocentrisme.

Il énonça trois lois qui décrivent les orbites des planètes autour du Soleil dans le référentiel héliocentrique (supposé galiléen). Ces lois peuvent être étendues aux comètes, ainsi qu’à tout satellite du Soleil (astéroïdes, etc.). La condition est que la masse m du corps étudié soit négligeable devant celle du Soleil, ce qui est vérifié pour tout corps du système solaire, y compris Jupiter.
Elles ont permis la formalisation par Newton de la loi de gravitation universelle. Isaac Newton les démontra à l’aide de sa nouvelle théorie de la gravitation.

Première loi de Képler

Chaque planète décrit une ellipse autour du Soleil qui occupe l'un des deux foyers

Une ellipse de foyers F et F’, désigne l’ensemble des points M du plan tels que FM + MF’ = constante.
Le centre O de l’ellipse est situé au milieu du segment [FF’].
On définit deux axes passant par O : l’un passe par F et F’, et l’autre est perpendiculaire au premier axe.
Les longueurs OA et OC sont égales et sont notées a, qui est le demi-grand axe de l’ellipse.
On a aussi OB = OD = b, avec b qui est le demi-petit axe.

Pour un corps en orbite autour du Soleil, l’aphélie est la position de l’orbite pour laquelle la distance entre le Soleil et le corps étudié est maximale, et le périhélie est la position de l’orbite telle que cette distance soit minimale.

L'ellipticité des orbites des planètes est très faible. La différence entre le cercle et l'orbite de la Terre est infime : si on veut la représenter sur une feuille de papier, la différence entre le cercle et l'ellipse tient dans l'épaisseur du trait de crayon ! Heureusement le Soleil n'est pas au centre de l'ellipse, mais au foyer qui est décentré.

Remarques :

• Il ne faut pas confondre périhélie et aphélie avec périgée et apogée, qui sont les termes équivalents pour des satellites de la Terre.
• Un cercle est une ellipse particulière pour laquelle les deux foyers F et F’ sont confondus et situés en O. Dans ce cas, on a a = b, et la relation FM + MF’ = constante devient OM = R, où R est le rayon du cercle.


• Dans la réalité, les orbites des planètes du système solaire sont des ellipses qui ressemblent beaucoup à des cercles.
• La première loi de Kepler est également applicable aux comètes. Les orbites observées sont dans ce cas très « étirées ».

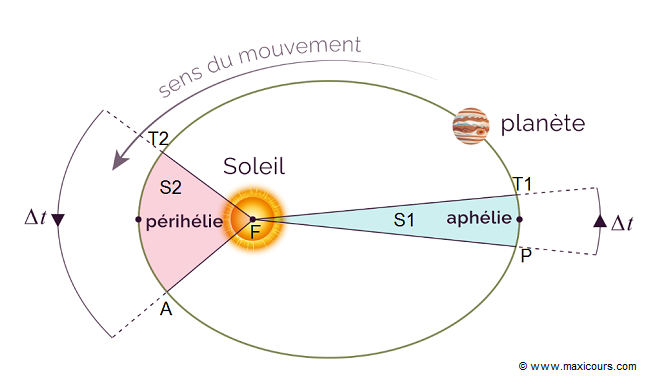
Deuxième loi de Képler - loi des aires

Dans le mouvement elliptique des planètes, leur rayon vecteur balaie des aires égales en des temps égaux

Le rayon vecteur est le segment de droite qui relie la planète au Soleil, sa longueur est variable.

Les deux triangles curvilignes F-P-T1 et F-T2-A ont la même surface, soit S1 = S2.

La 2ème loi de Képler implique que ces surfaces, étant égales entre elles, ont été balayées en des temps égaux.

La planète a donc mis le même temps pour aller de P à T1 que pour aller de T2 à A. Comme on peut le constater, la distance T2-A est plus grande, donc la vitesse moyenne sur ce trajet est plus élevée.

La planète a donc une vitesse variable sur son orbite, suivant l'endroit de celle-ci où elle se trouve. Elle est plus élevée au périhélie (point P) qu'à l'aphélie (point A). En pratique, les planètes se déplacent d'autant plus vite sur leur orbite qu'elles sont proches du Soleil.

Sur le schéma ci-dessus, on a représenté l’aire balayée pour deux positions distinctes, mais dans un même laps de temps Δt. La deuxième loi de Kepler se traduit par l’égalité des aires rose et bleue.

Troisième loi de Képler - loi des périodes

Le carré de la période de révolution d'une planète est proportionnel au cube du demi-grand axe de l'orbite elliptique.

Cette loi établit la relation entre deux grandeurs caractéristiques du mouvement d’une planète : sa période de révolution T, et le demi-grand axe "a" de son orbite.

Pour toutes les orbites planétaires le rapport du carré des périodes de révolution (p) au cube du demi-grand-axe de l'orbite (a) est constant.

On peut exprimer :

• "a" en Unités Astronomiques (en abrégé UA, 1 UA = 149 600 000 km),
• "p" en années,
• "K" est une constante.

La troisième loi de Képler s'applique aussi, avec la même valeur de K, aux astéroïdes et aux comètes du système solaire.

On peut l'appliquer à un ensemble de satellites orbitant autour d'une planète, comme Jupiter ou Saturne, entre autres, mais en redéfinissant la valeur de K pour chacun des systèmes.

La troisième loi de Képler permet, connaissant la valeur de K et la période de révolution d'un astre, de calculer sa distance.

Connaissant le temps de révolution d'une planète, la troième loi de Képler permet d'en tirer immédiatement la distance moyenne au Soleil (équivalent du demi-grand axe de l'orbite) en prenant pour unité la distance moyenne Terre-Soleil (l' UA mesure 149 600 000 km).
Par exemple, Saturne accomplit sa révoultion autour du Soleil en 29,46 années, sa distance moyenne au Soleil est donc égale à :

Généralisation des lois de Képler

Ces lois, obtenues dans le cas particulier du système solaire, se généralisent à tout système analogue, correspondant à un potentiel central. L'objet considéré, dans ce potentiel, ayant une masse m très inférieure à la masse M du potentiel central, et n'étant pas perturbé par d'autres satellites de M, présente alors les propriétés suivantes :

• Sa trajectoire autour de M est plane, elliptique, avec M à l'un des foyers.
• La loi des aires fournit l'évolution horaire du mouvement
• Le rapport du carré de la période de rotation au cube du demi-grand axe est identique pour tous les satellites de M.

Accueil - Liens utiles - Contact