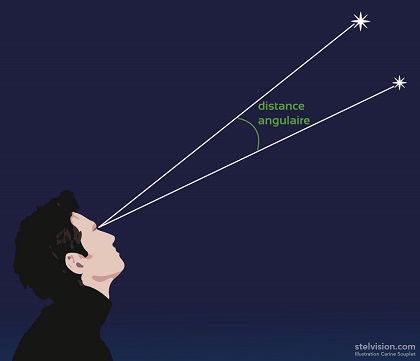
Mesurer les séparations angulairesLorsqu’on observe le ciel, on veut souvent mesurer l’écart entre deux objets. On mesure alors la séparation angulaire (appelée aussi distance apparente), qui est la valeur de l’angle formé entre les deux droites qui relient ces deux objets à l’observateur. Voici comment apprivoiser facilement cette mesure à l’œil nu !
Il est cependant bon de rappeler que lorsque nous mesurons l’écart entre deux astres dans le ciel, nous ne faisons qu’évaluer leur distance
apparente vue depuis la Terre. Il ne s’agit pas de l’éloignement réel entre ces deux objets. Quel est le diamètre apparent de la Lune ?
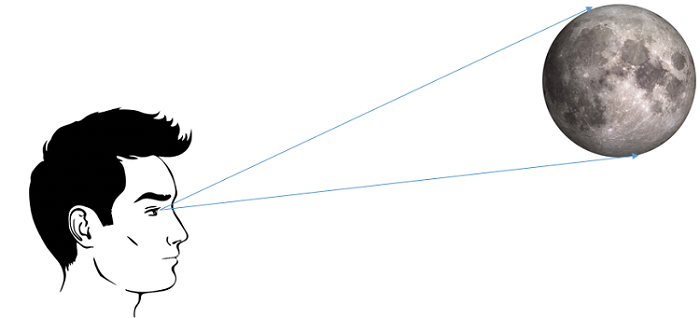
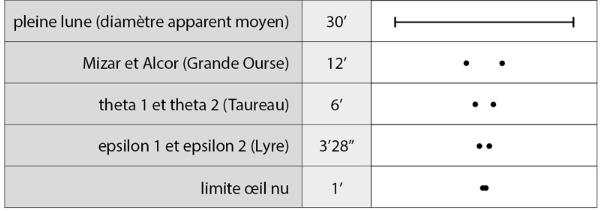
Le diamètre apparent de la pleine Lune, c'est-à-dire la séparation angulaire entre ses deux bords opposés mesure un demi-degré, soit 30 minutes. Une séparation angulaire se mesure en degrés, minutes et secondes d’arc
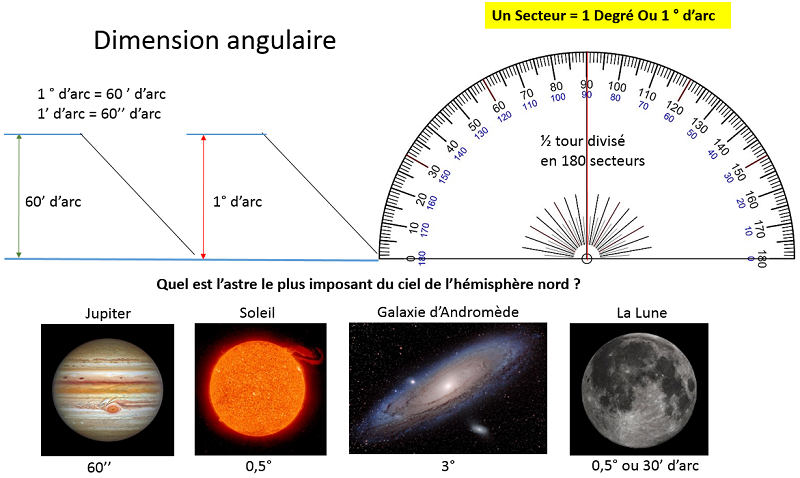
La sphère céleste au dessus de nous peut se diviser en 380 secteurs égaux que l'on va nommer des degrés d'arc.
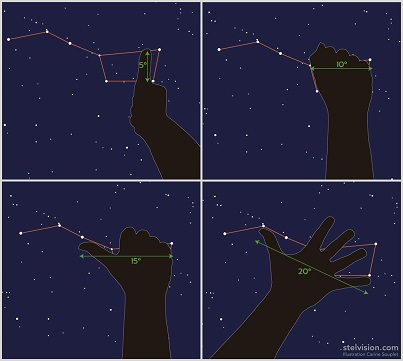
En utilisant sa main, l’observateur peut évaluer des distances
Nos yeux peuvent voir de petites séparations angulairesPour des valeurs en dessous de 1 degré, on admet que la séparation angulaire devient serrée à l’œil nu, cependant les limites de l’œil sont loin d’être atteintes ! En effet, le pouvoir de résolution de l’œil humain est d’environ 1’. Cela signifie que deux points séparés par moins de 1’ seront vus comme un seul et même point. Les deux étoiles Mizar et Alcor, dans la Grande Ourse sont elles aussi facilement discernables, alors qu'elles sont éloignées de 12 minutes, soit un peu plus du tiers de la pleine lune.
Ce moyen facile à mettre en œuvre permet par exemple de mesurer la hauteur d’un astre au-dessus de l’horizon ou l’éloignement entre une planète
et la Lune. Accueil - Liens utiles - Contact . |