La parallaxe en astronomie

Accueil du site

Qu'est-ce que la parallaxe ?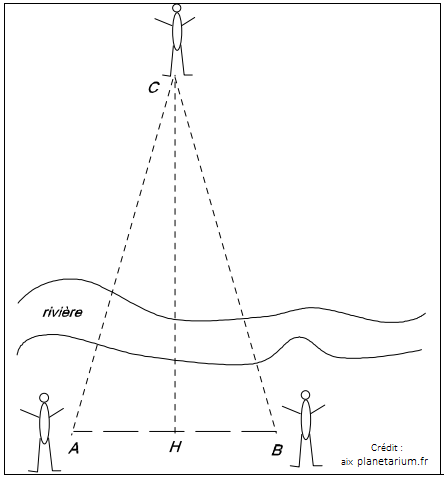

Une expérience courante est la suivante : on place devant soi le bras tendu et le pouce relevé, devant un fond relativement lointain. Si l’on regarde son pouce (sans le déplacer) successivement avec l’œil droit, puis avec l’œil gauche, on a l’impression qu’il se déplace devant le fond qui lui, reste immobile. L’illusion provient de ce que le pouce est observé sous deux angles différents par chacun des deux yeux, alors que le fond est trop lointain il semble donc immobile.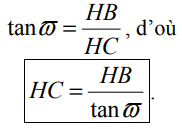

On dispose là d’un moyen très commode pour évaluer une distance hors de portée, rien qu’en connaissant une longueur de base et un angle.

Deux personnages respectivement en A et B aperçoivent un troisième personnage situé en C, de l’autre côté d’un rivière infranchissable. A et B désirent connaître la distance qui les sépare de C ; ils sont capables de mesurer la distance entre eux deux et de mesurer des angles en A ou B du triangle ABC (par exemple avec un théodolite).

Désignons par H le milieu de [AB] et par ϖ la mesure de l’angle BCH ; cet angle est le complément de HBC, que peuvent mesurer les observateurs en A et B. On supposera le triangle ABC isocèle. La trigonométrie permet d’écrire :

La parallaxe en astronomie

En astronomie, la parallaxe est l’angle sous lequel on pourrait voir une longueur connue, depuis un astre quelconque. On distingue généralement deux types de parallaxe : la parallaxe diurne et la parallaxe annuelle. La parallaxe diurne est utilisée pour les objets du Système solaire : c’est l’angle sous lequel on voit, depuis l’un d’entre eux, le rayon terrestre. La parallaxe annuelle est utilisée pour les étoiles (proches) : c’est l’angle sous lequel on voit le demi-grand axe de l’orbite terrestre depuis une étoile. Cette parallaxe d’étoiles a été mise en évidence pour la première fois en 1838 par F. Bessel.

Détermination de la parallaxe diurne d’une planète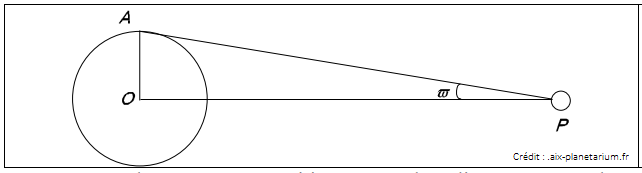

Le rayon terrestre OA est vu, depuis la planète P sous un angle ϖ , appelé parallaxe diurne de P.

Deux observateurs se positionnent en deux lieux sur Terre, les plus éloignés possible, et mesurent la position de la planète. Ils en déduisent la parallaxe diurne de celle-ci.

Détermination de la parallaxe annuelle d'une étoile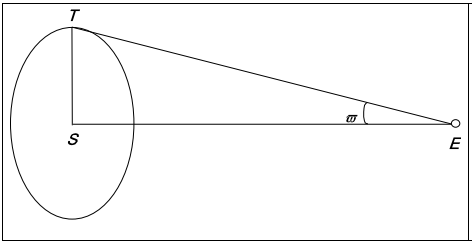

Le demi-grand axe de l’orbite terrestre ST (S pour Soleil et T pour Terre) est vu depuis une étoile E sous un angle ϖ, appelé parallaxe annuelle de E.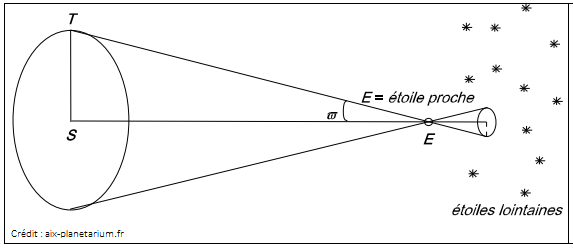

À six mois d’intervalle, une étoile proche n’apparaît pas exactement à la même place dans le ciel par comparaison avec les étoiles lointaines qui nous semblent immobiles. Il semble que l’étoile proche décrive une ellipse dont le demi-grand axe, mesuré généralement en seconde d’arc est la parallaxe de cette étoile. Connaissant la valeur moyenne de la distance Terre-Soleil, on en déduit facilement la distance de l’étoile au Soleil, qui est, à cette échelle, la même que la distance de l’étoile à la Terre.

S représente le Soleil et T la Terre. L’étoile « proche » E semble décrire, en six mois d’intervalle, une petite ellipse par rapport aux étoiles plus lointaines. Le demi-grand axe de cette ellipse apparente, mesurée en secondes d’arc, est la parallaxe annuelle de E.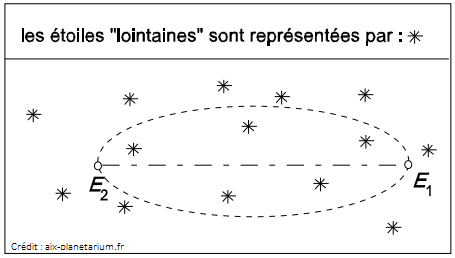

Par rapport à des étoiles « lointaines » (qui semblent de ce fait immobiles), l’étoile proche E semble décrire une ellipse : à six mois d’intervalle, elle occupe par rapport à ces étoiles lointaines, les deux positions E1 et E2. Connaissant l’échelle du cliché, on peut exprimer la distance E1E2 en secondes d’arc : c’est le double de la parallaxe ϖ de E. Typiquement, la parallaxe d’une étoile est inférieure à 1".

Expression pratique de la parallaxe d’une étoile

Une nouvelle unité de distance : le parsec

De manière à encore simplifier les calculs, on définit en astronomie une nouvelle unité de distance : le parsec (pc). Définition : : On dira qu’une étoile est située à 1 pc si sa parallaxe est égale à 1 seconde d’arc. En d’autres termes, depuis cette étoile (située à 1 pc), on verrait le demi-grand axe de l’orbite terrestre (1 UA, c’est-à-dire 150 millions de km) sous un angle de 1" (seconde d’arc, 3 600e partie du degré). Déduisons de cette définition la valeur de 1 pc en UA :

Conclusion : Si la parallaxe d’une étoile est exprimée en secondes d’arc, son inverse est la distance de cette étoile exprimée en pc.

Les prouesses du satellite Hipparcos

Jusque vers les années 1980, la méthode de la parallaxe annuelle avait permis de mesurer la parallaxe d’environ 8 000 étoiles. En août 1989, la satellite HIPPARCOS (pour High Précision PARallaxe Collection Satellite) a été placé sur une orbite très elliptique (initialement, il devait être placé sur une orbite géostationnaire, mais une panne de l’un des moteurs empêcha la manœuvre) et a ainsi pu mesurer avec une précision de l’ordre de la milliseconde d’arc, la parallaxe de 120 000 étoiles.

Accueil - Liens utiles -